2023
Rochester, United States
Moon formation project
I am currently coding time-efficient numerical simulations to be able to form the Moon from a realistic protolunar disk.
My code is able to detect collisions between the moonlet in a time proportionnal to the total number of moonlets, which will
eventually allow me to simulate protolunar disk with hundreds of thousands of moonlets.
This work is still in progress and the simulations displayed here are trials with only some parts of the code working. A PDF document
of the mathematical model, as well as the algorithm used for collision detection, is available here.
The C language is used for the numerical simulation, while python and ffmpeg are used to create the animations.

N = 80
Earth center of mass
A very early test, mainly to verify that the code is working normally, and to see the rendering of the animations. Not all moonlets have the same size, but size differences are not displayed in this animation. Here, the moonlets only interact with the center of mass of the Earth (shown by the grey circle).
N = 140
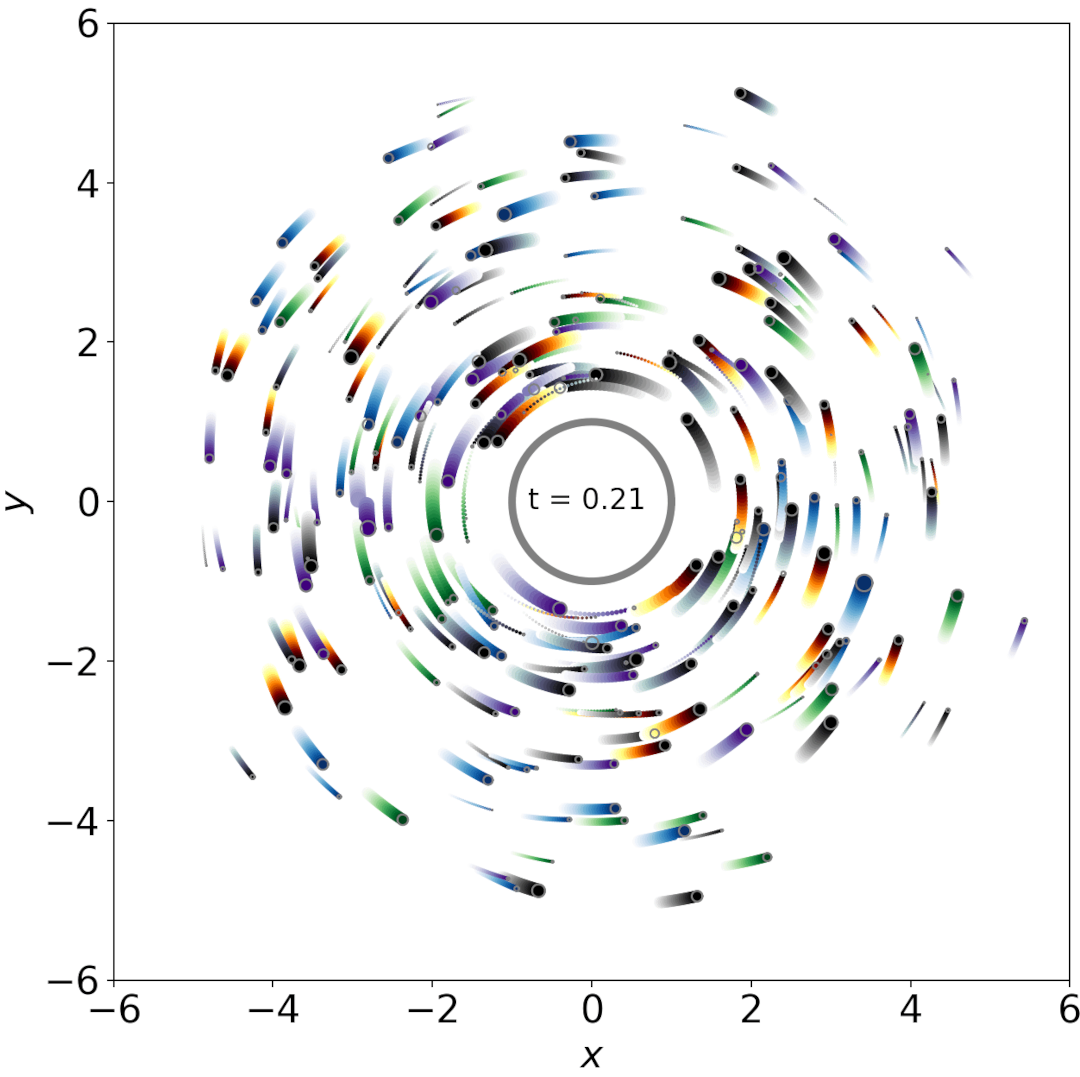
Elastic collisions
Here, besides their interaction with the center of mass of the Earth, the moonlets also interact through elastic collisions and behave like bouncing balls. The moonlets are displayed with their true radius. The time is in units of the surface orbital period.
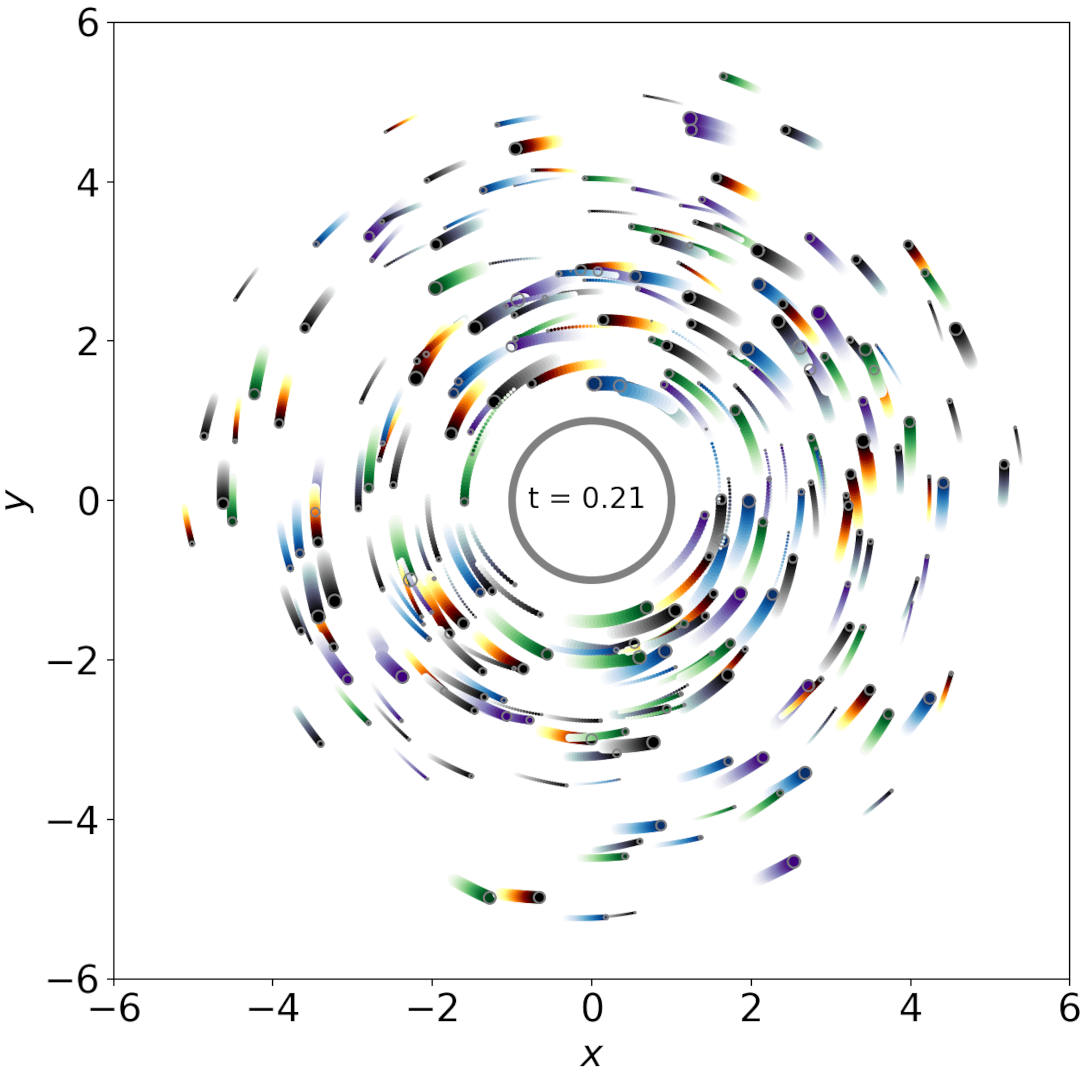
N = 250
f = 1.7
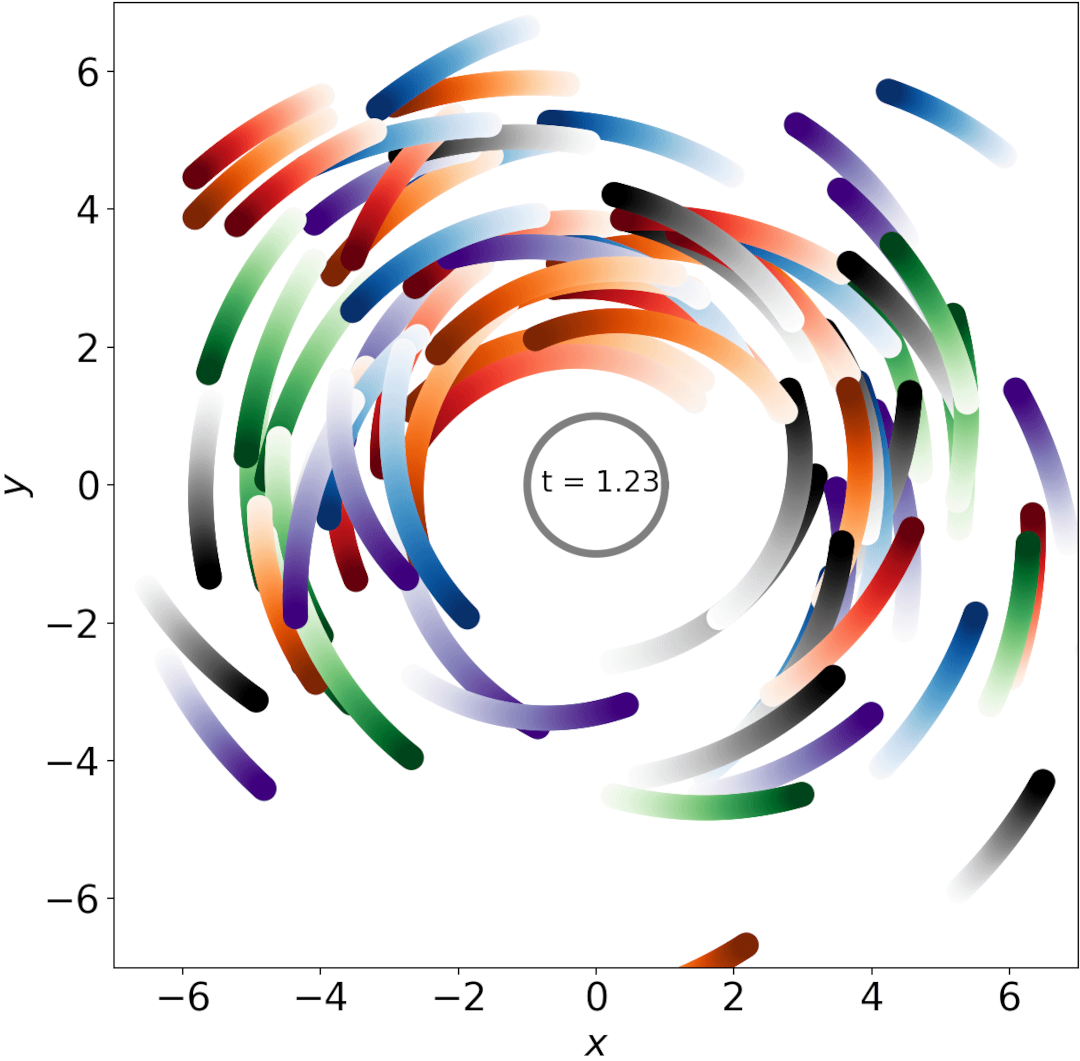
Inelastic collisions
The inelasticity of the collisions can be controlled by a parameter that I call f (see here). For f=2, the collision is elastic (perfect bouncing), while for f=1, the collision is completely inelastic (no bouncing at all). The moonlet merge if their relative velocity after impact is less than their escape velocity.
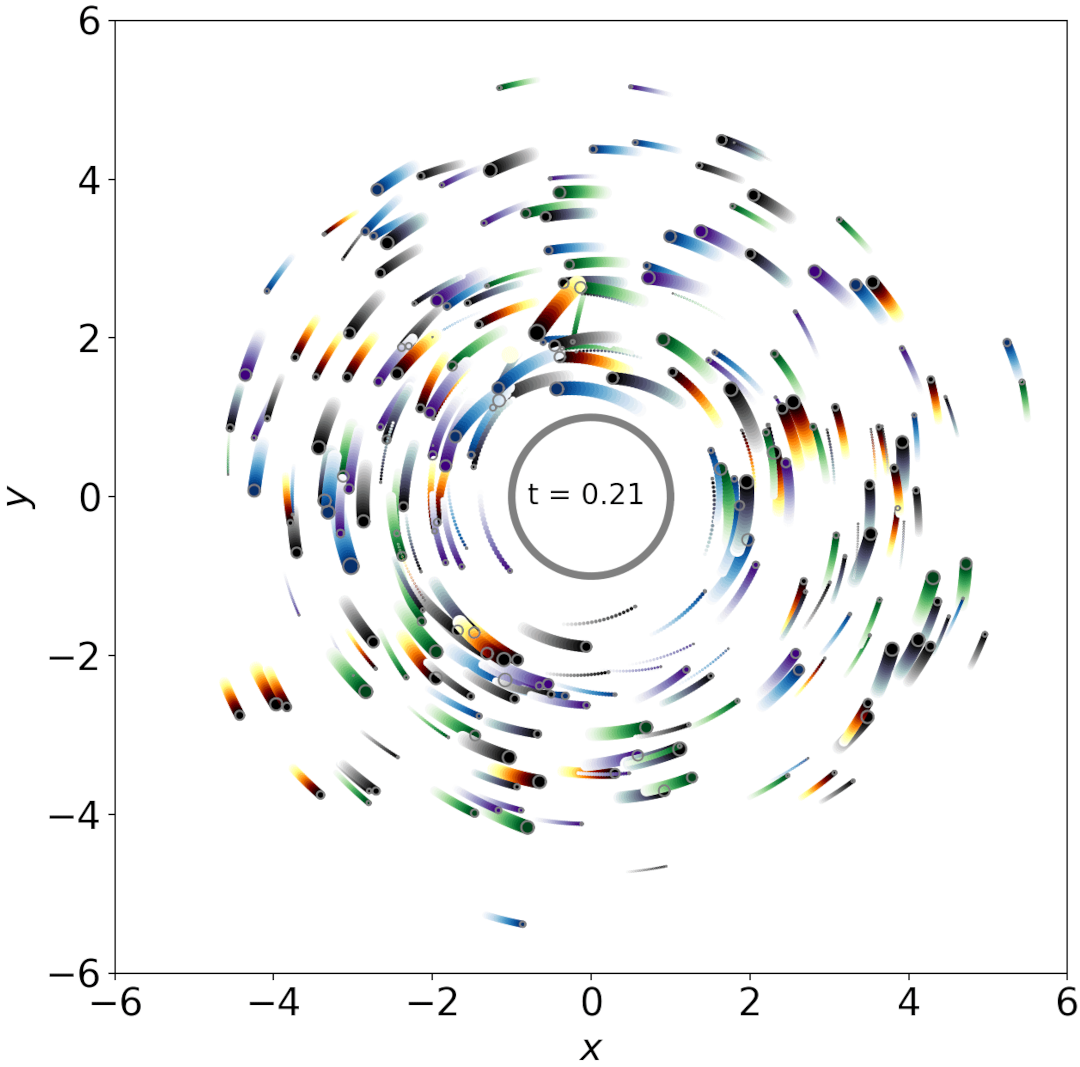
N = 250
f = 1.5
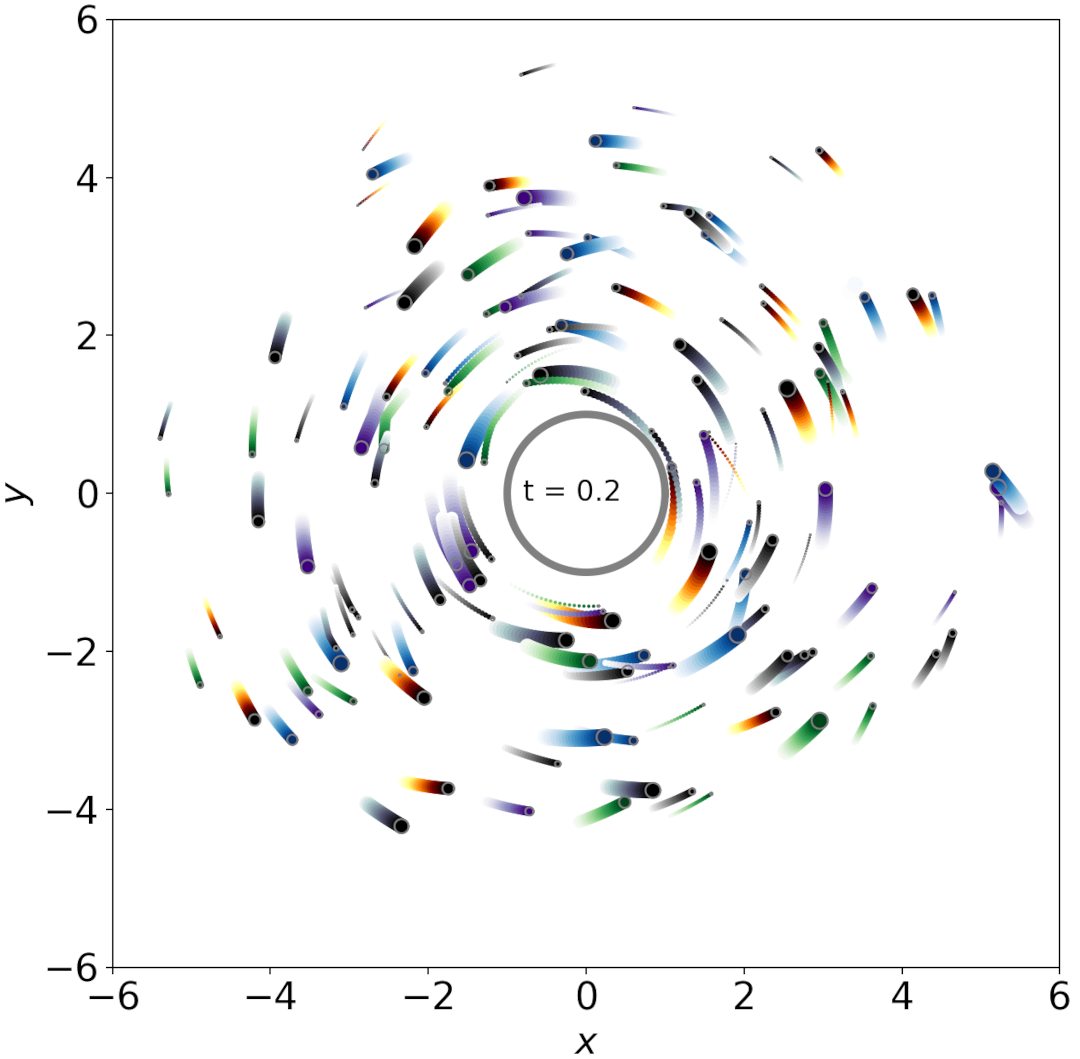
Inelastic collisions
Here, f is 1.5 and the collision are less elastic than in the above simulation.
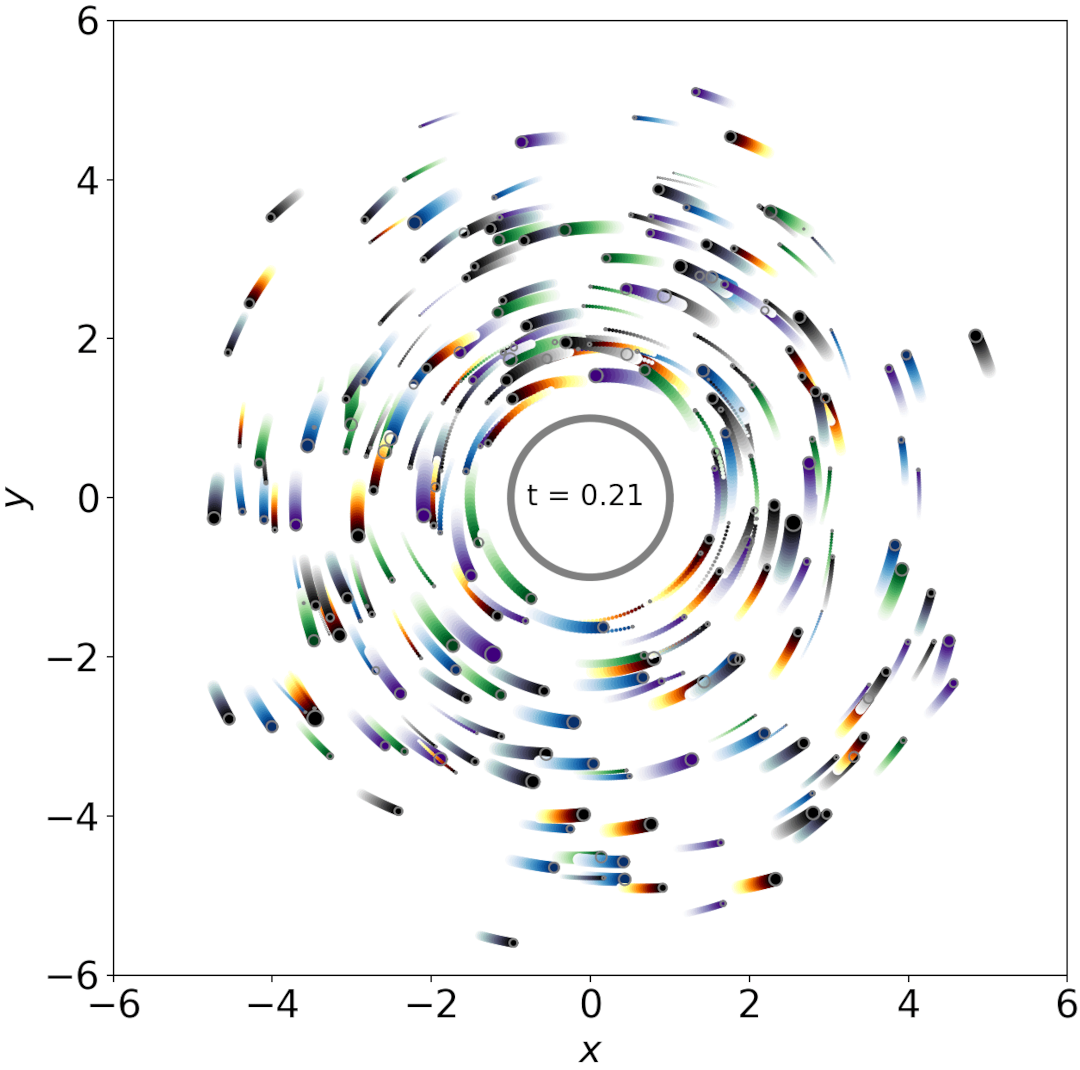
N = 250
f = 1.3
Inelastic collisions
Here, f is 1.3 and the collision are even less elastic than in the above simulation. Moonlet merging becomes common.
N = 250
f = 1.1
Very inelastic collisions
Here, f is only 1.1 and the collisions are very inelastic. Most collisions lead to moonlet merging.