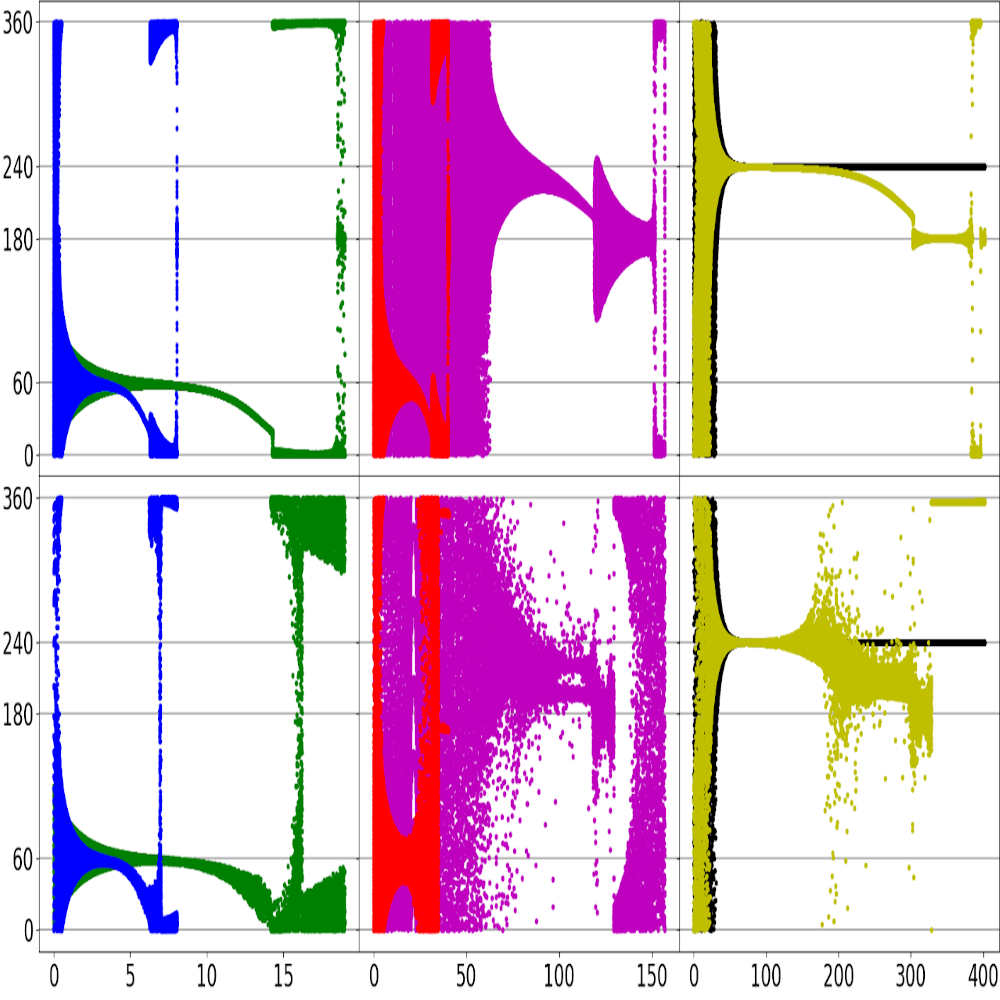
Motion of particules around a Schwarzschild black hole
The following gifs were created from numerical integration of the equations of geodesics in the Schwarzschild's metric. The central black hole is
of one solar mass and the axes are in kilometers. The coordinate time was used as the affine parameter in the integrations, meaning that the motion
of the massless particlues is the one seen by an asymptotic observer, that is someone at rest, located infinitely far away from the black hole,
were spacetime is flat. A Runge Kutta method of fourth order was especially coded.
The inner black circle is the event horizon of the black hole, located at one Schwarzschild radius from the singularity, or roughly 3 kilometers for a one solar mass black hole. The outer black circle is the radius of the innermost stable circular orbit (ISCO), located 3 Schwarzschild radii away from the singularity.
This work was done as part of a project during my second year of the master Dynamiques des systèmes gravitationnels at the observatory of Paris.
The inner black circle is the event horizon of the black hole, located at one Schwarzschild radius from the singularity, or roughly 3 kilometers for a one solar mass black hole. The outer black circle is the radius of the innermost stable circular orbit (ISCO), located 3 Schwarzschild radii away from the singularity.
This work was done as part of a project during my second year of the master Dynamiques des systèmes gravitationnels at the observatory of Paris.
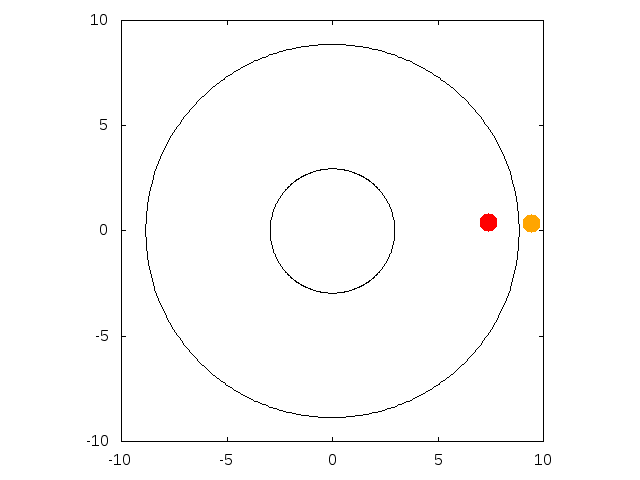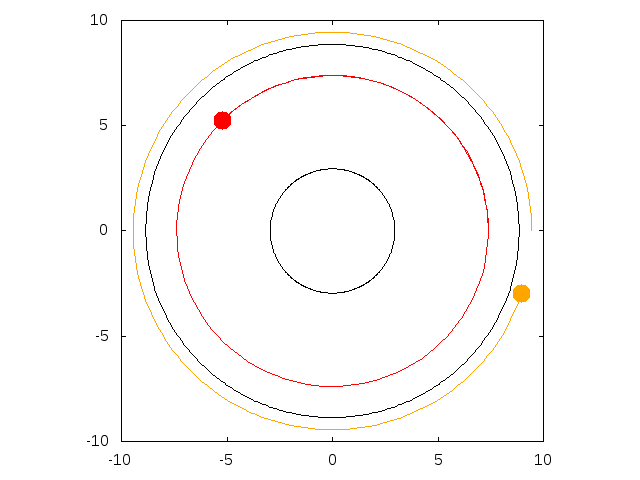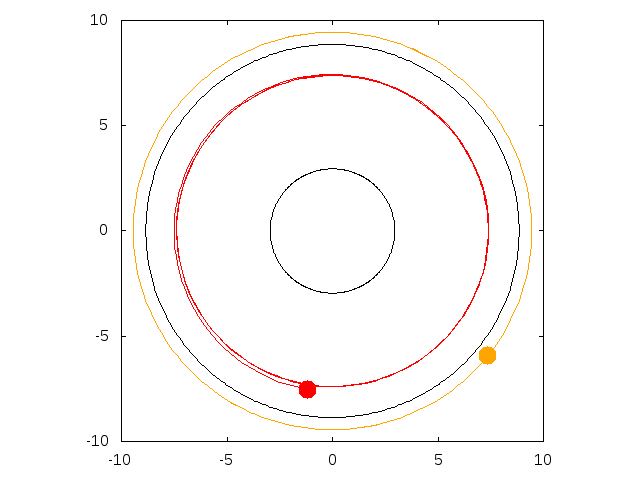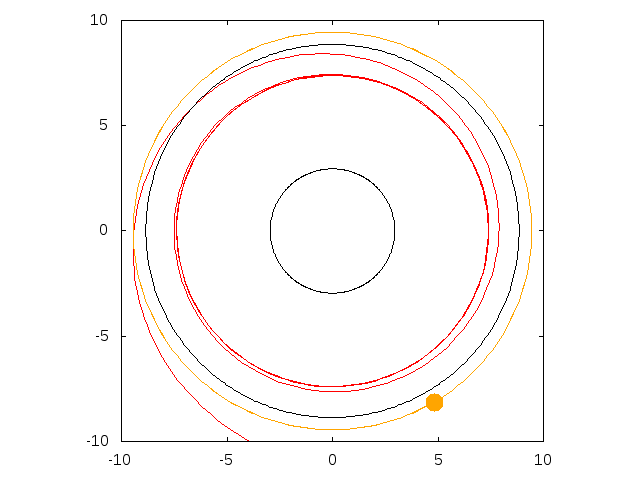
On the first animation, the red particule is on an unstable circular orbit since it is below the ISCO. When a particule leaves an unstable
circular orbit, it can either fall onto the singularity, or get away from the black hole. When it gets away, whether it stays bounded
to the black hole or goes to infinity, depends on the radius of the initially circular orbit. For orbits below 2 Schwarzschild radii,
the particule goes to infinity, while for orbits above, it stays bounded. On the second animation, the orange particule has a 2.1 Schwarzschild
radius and stays bounded while the red particule, with a 1.95 Schwarzschild radius initial orbit goes to infinity. When the apoapsis is not infinite,
its value depends only on the initial radius.
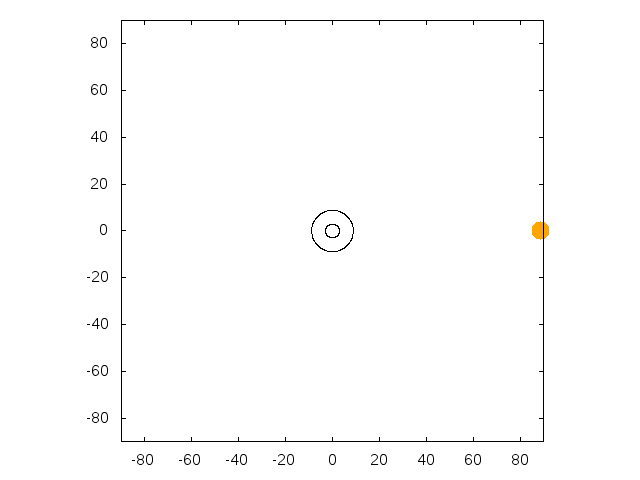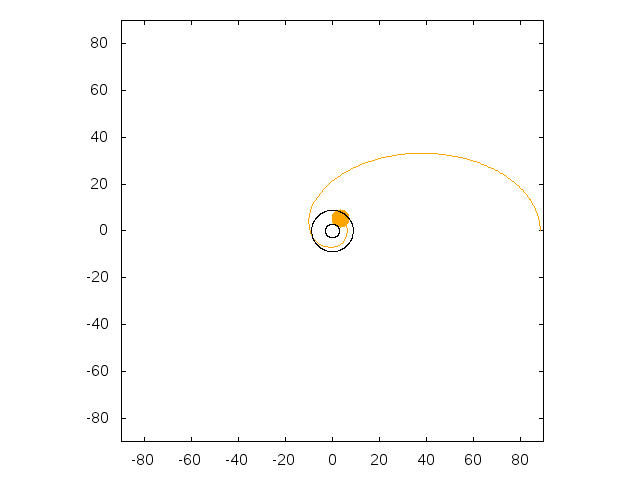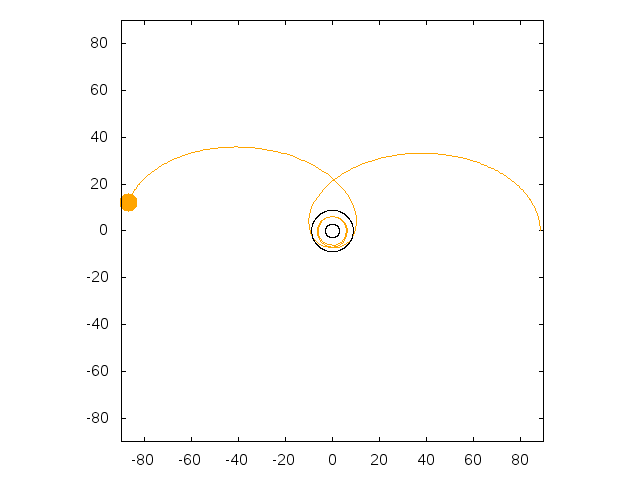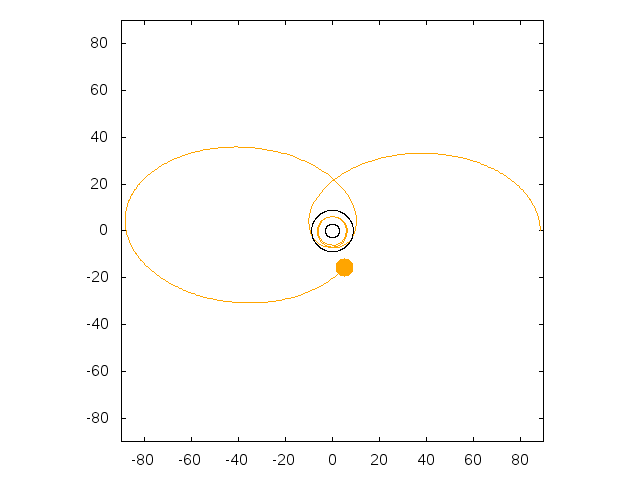
On the first animation, the particule is dropped from 30 Schwarzschild radii with an horizontal speed such that its periapsis is close to
the black hole, leading to a huge precession of the ellipse. On the other animation, the initial speed is chosen so that the particule settles on
an (unstable) circular orbit. The radius of the circular orbit is then determined only by the height of the apoapsis (here 30 Schwarzschild radii).